Paper notes-Cai Xindong Phd Thesis

文献阅读笔记 蔡昕东博士论文《光量子计算及其算法实现》

4个部分

1. 多自由度量子隐形传输
2. 量子求解线性方程组
3. 量子机器学习
4. 相位弱测量

##1 基本概念和技术 量子态叠加原理和量子比特 量子纠缠和量子隐形传态 光子极化是最常用的量子比特编码自由度。 对于光子极化量子比特的操纵和测量可以采用成熟的半波片技术：对光子极化的任意幺正旋转都可以由两块四分之一波片和和一块半波片实现；对于光子极化的测量则可以使用一块四分之一玻片、一块半波片、一个极化分束器和探测器的组合实现。 光子的其他自由度有路径、轨道角动量、频率和时间等。 纠缠光子对的产生。 当激光通过某些非线性晶体时，会有一定几率发生参量下转换(SPDC)过程，一个光子劈裂成两个低频光子对。为了弥补信号光和闲频光在空间和时间上出现的差异，需要进行补偿。

##2 多自由度量子隐形传输 信息同时编码在光子的极化和轨道角动量自由度上。发展了对于光子轨道角动量的高效率操控和测量技术手段，以及多自由度的联合操纵技术，首次实现了轨道角动量的多光子纠缠。

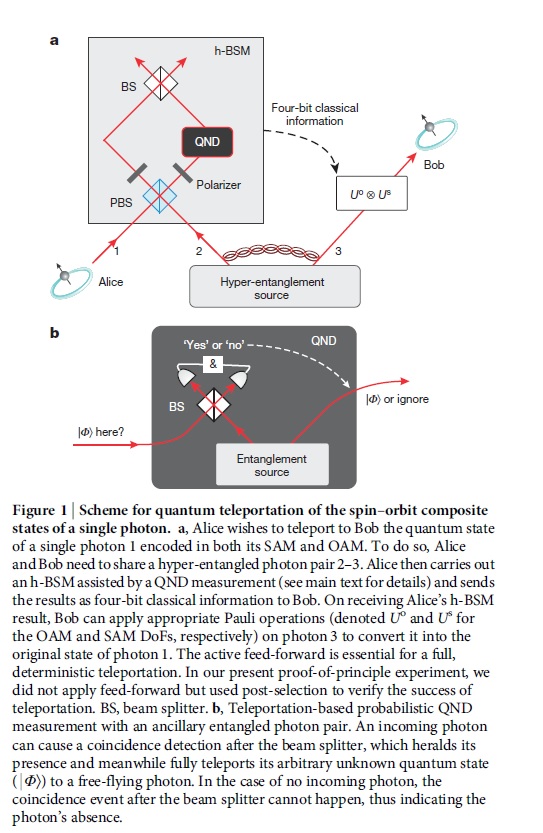
两个干涉结构不能简单地级联，解决方案是利用量子非破坏性测量。

##3 量子求解线性方程组 量子计算机通过将经典数据编码在量子态希尔伯特空间中，理论上能够实现指数级的加速。 解线性方程组问题是：在给定向量$\vec{b}$和矩阵$A$的条件下，求解向量$\vec{x}$，满足$A\vec{x}=\vec{b}$。或者等价表示为，求解向量$\vec{x}=A^{-1}\vec{b}$。把输入态和输出态在矩阵$A$的本征态上展开，可以得到输出向量$|x\rangle = A^{-1}|b \rangle = A^{-1}\sum_{j}\beta_{j}|u_j\rangle = \sum_{j}\frac{\beta_j}{\lambda_j}|u_j\rangle$。 可见输出向量x和输入向量b的区别在于每一个本征态前面额外添加了一个对应的本征值倒数作为系数，因此求解线性方程组的目的就可以转化为如何得到这些本征值信息并将其加在对应的本征态分量上。获得这些本征值信息又如何把本征值信息添加到相应的本征态的分母上去就分别是量子线性方程算法的第一步和第二步。

第一步可以将如何获得本征值信息的问题转化为一个标准的相位估计问题。由于该过程是量子并行的，因此可以体现出算法的加速。所有的$\lambda_j$是一起算出来的，这一步是整个算法的核心，是量子加速的根源。但最终需要$\lambda_j$作为系数的分母存在。

算法的第二步是将量子态$$

\lambda_j\rangle$变成系数$\frac{1}{\lambda_j}。这一步需分为三小步，第一小步，将本征值的量子态变成其倒数的量子态，需要额外的辅助比特和受控门。第二步让辅助比特在寄存器的受控操作下进行态演化。第三小步再将寄存器取倒数，此时本征值在受控门的作用下抽取并存储于系数的分母中了。

算法的第三步进行反相位估计，将寄存器比特解纠缠，恢复到初始状态，。再测量辅助比特，选择特定结果，就得到所需要的矢量。整个量子算法的时间复杂度为$O(log(N)s^2k^2/e)$, 其中k是条件数，也即矩阵A的最大本征值和最小本征值的比值，e是输出向量的可接受的的误差率。算法获得指数加速的提升。

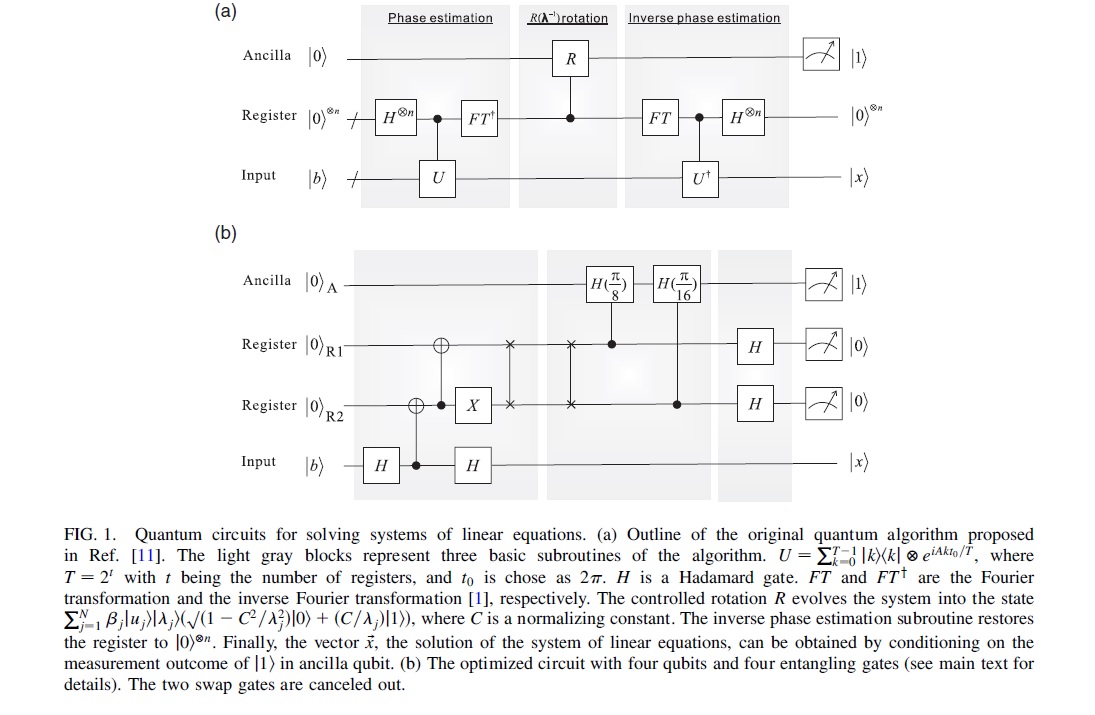
##4 量子机器学习

机器学习简介： 有监督机器学习/无监督机器学习

分类算法： 平均值分类算法/近邻分类算法

量子机器学习

Seth Lloyd提出量子计算机可用于解决有监督和无监督的机器学习问题，并获得指数加速。量子机器学习加速的核心思想就是快速计算距离，在$O(log(MN))$的时间复杂度完成计算。

##5 相位弱测量 干涉仪是用于测量光学相位的最重要的精密测量设备之一。诸多物理量的测量都可以转化为对于相位的测量。在干涉仪中，相位分辨率通常有两方面的误差，一是统计误差，二是系统误差。统计误差原则上可以通过多次重复测量来不断地减小。因此在实际测量中，对最终分辨能力起决定性作用的很多时候是系统误差。弱测量通过借助于量子效应，可以有效地放大微笑物理量，提高对各个物理量的分辨精度，降低系统误差的影响。

理想干涉仪

在标准的干涉仪中，两臂的微笑相位差可以通过测量某一个输出口的光子概率获得。输出口的光子探测概率为：

$$p\propto \frac{1}{2}(1+cos(\phi+\varphi))

其中，$\phi$是待测量的微小相位，$\varphi$是干涉仪其中一臂的可调节相位。

考虑干涉仪自身噪声后的测量精度

使用N00N态不能降低系统噪声带来的相位不确定性。

弱测量方案

在一个实际的干涉仪中，对于最后测量结果的不确定性，系统噪声往往起着决定性的作用，也即$\rho\gg 1/ \sqrt{N}$。因此，要提高最终结果的分辨能力，降低系统内在噪声的影响起着至关重要的作用。弱测量手段是用于降低实验系统噪声的重要手段。

Ref:

[1] Wang, X.-L. et al. Quantum teleportation of multiple degrees of freedom of a single photon. Nature 518, 516–519 (2015).

[2] Harrow, A., Hassidim, A. & Lloyd, S. Quantum Algorithm for Linear Systems of Equations. Phys. Rev. Lett. 103, 150502 (2009).

[3] Cai, X.-D. et al. Experimental Quantum Computing to Solve Systems of Linear Equations. Phys. Rev. Lett. 110, 230501 (2013).

[4] Rebentrost, P., Mohseni, M. & Lloyd, S. Quantum Support Vector Machine for Big Data Classification. Phys. Rev. Lett. 113, 130503 (2014).

[5] Cai, X.-D. et al. Entanglement-Based Machine Learning on a Quantum Computer. Phys. Rev. Lett. 114, 110504 (2015).

[6] Li, Z., Liu, X., Xu, N. & Du, J. Experimental Realization of a Quantum Support Vector Machine. Phys. Rev. Lett. 114, 140504 (2015).